TERMOLOGIA
01.(UECE 83.1) Duas escalas termométricas lineares estão representadas na figura ao lado. Uma graduada em 0X e a outra 0Y. O ponto 100 da escala X corresponde ao ponto 80 na escala Y; onde a escala X marca 0X, a escala Y marca 200Y. Assim, quando a escala X marcar 500X, a escala Y marcará:
a) 300Y b) 400Y c) 500Y d) 600Y
(50 – 0)/(100 – 0) = (TY – 20)/(80 – 20) → 50/100 = (TY – 20)/60
→ 1/2 =
(TY
– 20)/60 → 1 = (TY – 20)/30
→ TY – 20 = 30
→ TY = 20 + 30
= 500Y.
02. (UECE 87.1) Comparando-se a escala (E) de um termômetro com a
escala C (Celsius), obteve-se o seguinte gráfico de correspondência entre as
medidas. Quando o termômetro Celsius estiver registrando 900C, o
termômetro (E) estará marcando:
a) 1000E b) 1200E c) 1500E d) 1700E
(90 – 0)/(50 – 0) = (TE + 10)/(90 + 10) → 90/50 = (TE + 10)/100
→ 90 =
(TE
+ 10)/2 → 180 =
TE
+ 10 → TE = 180 – 10
= 500E.
03. (UECE 84.2) Mergulham-se dois termômetros na água; um graduado na
escala Celsius e o outro na escala Fahrenheit. Espera-se o equilíbrio térmico e
nota-se que a diferença entre as leituras nos dois termômetros é igual a 92. A
temperatura da água valerá, portanto:
a) 280C; 1200F b) 320C; 1240F c) 600C; 1520F d) 750C;
1670F
I. TF – TC = 92 → TF = 92 + TC.
II. TC/5 = (TF – 32)/9 → TC/5 = (92 + TC – 32)/9 → TC/5 = (TF
+ 60)/9 → 9TC
= 5TC + 300 → 4TC = 300 → TC = 300/4 = 750C.
III. TF = 92 + TC
= 92 + 75 = 1670F.
DILATAÇÃO
04. (UECE 86.1) Assinale a única afirmativa correta
:
a) Caloria é unidade de intervalo de
temperatura.
b) Um corpo com temperatura 800C é
duas vezes mais quente que outro com temperatura de 400C.
c) O coeficiente de dilatação linear, térmica,
depende do comprimento do corpo.
d) Os coeficientes de dilatação
linear e superficial podem ser medidos com uma mesma unidade.
05. (UECE 92.1) Um pino metálico, a uma dada temperatura, ajusta-se
perfeitamente em um orifício de uma placa metálica. Se somente a placa for aquecida,
verifica-se que:
a) O pino passará mais facilmente pelo orifício.
b) Haverá contração apenas do orifício da placa.
c) O pino não mais passará pelo orifício.
d) É impossível prever o efeito, desconhecendo o coeficiente de
dilatação linear dos dois metais.
06. (UECE 99.1) Uma linha férrea tem
trilhos cujo coeficiente de dilatação linear é α. Os trilhos são assentados com comprimento L0
à temperatura t0. Na região, a temperatura ambiente pode atingir o
máximo valor t. Ao assentarem os trilhos,
a mínima distância entre as extremidades de dois trilhos consecutivos
deverá ser:
a) L0αt b) 2L0α( t – t0) c)
L0α( t – t0)/2 d) L0α (t
– t0)
07. (UECE
2011.1.F2) Dois líquidos LI e LII são submetidos a
variações de temperatura, de modo que LI seja aquecido de 2 °C e LII
sofra uma redução de 2 °C na sua temperatura. Verifica-se que o aumento de
volume de LI é igual, em módulo, à variação de volume de LII.
Assim, pode-se afirmar corretamente que
a) se os dois volumes de líquido forem iguais antes das variações de
temperatura, os coeficientes de dilatação são os mesmos para ambos os líquidos.
b)
se, antes das variações de temperatura, o volume do líquido I for maior que o
do II, o coeficiente de dilatação do I é maior do que o do II.
c)
se, antes das variações de temperatura, o volume do líquido I for menor que o
do II, o coeficiente de dilatação do I é menor que o do II.
d)
se os dois volumes de líquido forem iguais antes das variações de temperatura,
os coeficientes de dilatação são diferentes para ambos os líquidos.
CALORIMETRIA
08. (UECE 81.1) Cedem-se 684 cal a 200 g
de ferro que estão a uma temperatura de 100C. Sabendo-se que o calor
específico do ferro vale 0,114 cal/0C, concluímos que a temperatura
final do ferro será:
a) 100C b) 200C c) 300C d) 400C
Q = m.c.Δθ → 684 = 200.0,114.Δθ → Δθ = 684/22,8 = 300C.
Δθ = θ – θ0 →
30 = θ – 10 → θ = 30 + 10 = 400C.
09. (UECE 83.1) O gráfico abaixo indica a
variação da temperatura de 1,0 g de uma substância em função da quantidade de
calor que lhe é fornecido. A substância está primitivamente no estado sólido. O
calor de fusão da substância é, em cal/g:
a)
5 b) 30 c) 45 d) 60
Q = m.Lf → 30 =
1.Lf → Lf = 30 cal/g.
10. (UECE 92.2) Um calorímetro, cujo
equivalente em água é igual a 35 g, contém 115 g de água à temperatura de 200C.
Colocam-se, então, no calorímetro, mais 300 g de água à temperatura de 500C.
A temperatura de equilíbrio térmico é:
a) 400C b) 500C c) 350C d) 200C
QA + QB
= 0 → mA.cA.(T
– 60) + mB.cB.(T – 10) = 0 → (35 +
115).1.(T – 20) + 100.1.(T – 50) = 0 → 150.(T – 20) + 300.(T – 50) = 0 → 150T – 3000 + 300T – 15000 =
0 → T =
18000/450 = 400C.
11. (UECE 95.1) O gráfico fornece a
variação de temperatura de uma substância, inicialmente no estado sólido, em
função da quantidade de calor que ela recebe. A massa da substância vale 5
gramas. A razão do calor específico da substância no estado sólido pelo seu
calor específico no estado líquido é:
a) 1/4 b) 1/3 c) 2/3 d) 3/4
I. No sólido: QS
= m.cS.ΔθS → 50 = 5.cS.40 → cS = 50/200 = 1/4 cal/g.0C.
II. No Líquido: QL
= m.cL.ΔθL → 100 = 5.cL.60 → cL = 100/300 = 1/3 cal/g.0C.
III. cS/cL = (1/4)/(1/3) = 3/4.
12. (UECE 99.2) Um corpo de
massa 400 g é aquecido através de fonte térmica de
potência 500 cal/min. constante. A temperatura do corpo, em função do tempo,
aumenta segundo o gráfico abaixo:
O calor específico do
material de que é feito o corpo é:
a) 0,615 cal/g.oC
b) 0,715 cal/g.oC
c) 0,625 cal/g.oC d) 0,725 cal/g.oC
P = Q/Δt
→ 500 = Q/10 → Q = 5000 cal.
Q = m.c.Δθ →
5000 = 400.c.20 → c = 5000/8000 = 0,625 cal/g.oC.
13. (UECE 2002.2) Em Fortaleza, em determinada hora do dia, a
radiação solar incidente pode chegar a valores de cerca de 800 W/m2.
Se 50% da energia coletada por um painel de energia solar de 4 m2 de
área pode ser aproveitada para aquecer a água contida em um tanque, o aumento
da temperatura após passada uma hora, se o volume de água no tanque é 2 m3
é aproximadamente igual a:
Dados:
Calor específico da água: c = 4.000 J/kgK
Densidade da água: d =1.000 kg/m3
a) 0,18ºC b)
0,36ºC c)
0,72ºC d) 1,44ºC
Pot TOTAL
= 800. 4 = 3200W
PÚTIL = PTOTAL . 50% =
1600W
Δt = 1h = 3600s V = 2m3 e d = 1000kg/m3
m = d . V = 1000 . 2 = 2 . 103kg
Q = m . c . Δθ
PÚTIL . Δt = m . c . Δθ
1600 . 3600 = 2 . 103 . 4 . 103
. Δθ → Δθ= 0,72oC.
14. (UECE 2006.2.F1) Em uma sala de
3 m de pé direito, o condicionador de ar é montado a, mais ou menos, 2 m do chão
(Posição P). É claro que é possível montá-lo a 1 m do chão (Posição Q). Montado
na posição P, o aparelho tem melhor desempenho em virtude, principalmente, da:
a) radiação
b) condução
c) convecção
d) radiação e da condução
GASES
15.
(UECE 85.1) Em condições
isotérmicas, determinada massa de um gás perfeito tem seu volume reduzido em
25%. A correspondente variação de pressão será, aproximadamente:
a) + 33% b) + 25% c) – 33% d) c) – 25%
P1.V1/T1 = P2.V2/T2
→
P1.V1 = P2.0,75.V1
→
P2 = P1/0,75
= 4.P1/3 = 1,33.P1 = P1 + 0,33P1.
16. (UECE
89.2) As lâmpadas elétricas de filamentos possuem no seu interior um gás
inerte. Admita que, ao ligar a lâmpada, a temperatura do gás eleva-se de 270C
para 1270C. Se a pressão inicial do gás é p, sua pressão final será,
supondo um comportamento de gás ideal:
a)
3p/4 b)
4p/3 c)
5p/4 d) 5p/3
P1.V1/T1
= P2.V2/T2
→
p/300 = P2/400
→
P2 = 4p/3.
17. (UECE 90.2) Um gás ideal sofre uma
transformação isobárica, ocorrendo duplicação da sua temperatura centígrada. É
correto afirmar que:
a) o volume do gás duplica.
b) a pressão do gás duplica.
c) o volume do gás permanece constante.
d) a velocidade média das
moléculas aumenta.
A duplicação em T em 0C
não implica na sua duplicação em kelvin, lembrando que VM2 = K.T, sendo k a constante de Boltzmann.
18. (UECE 93.2) O bico de uma
seringa de injeção é vedado, quando 1,0 cm3 de ar é encerrado no
interior da seringa, nas condições ambientais de temperatura e pressão. Agora,
puxa-se lentamente o êmbolo para fora. O gráfico ao lado representa a variação
da pressão do ar em função do volume. A transformação é isobárica e os atritos
são desprezados. A pressão p do gás, no estado final F, é em cm/Hg:
a) 15 b) 19
c) 25 d) 38
P1.V1/T1
= P2.V2/T2 → 76.1 = P.4 → P = 76/4 = 19 cmHg.
19. (UECE 98.1) Uma bomba de
bicicleta tem um comprimento de 24 cm e está acoplada a um pneumático.
Inicialmente, o pistão está recuado e a pressão do ar no interior da bomba é
1,0 atm. É preciso avançar o pistão de 8,0 cm, para que a válvula do pneumático
seja aberta. Quando isso ocorrer, a pressão, em atm, na câmara de ar, supondo
que a temperatura foi mantida constante, será:
a) 1,5 b)
2,0 c) 2,5 d) 3,0
P1.V1/T1 = P2.V2/T2 → 1.24.A = (24 – 8).A.P2 → P2 = 24/16 = 3/2 = 1,5 atm. (Obs.:
V = A.h)
20. (UECE
2012.1.F2) Um tanque com volume V contém
nO moles de oxigênio
e nN moles de
nitrogênio à temperatura T.
Sendo R a constante universal
dos gases e considerando-se que esses gases se comportem como gases ideais
dentro desse tanque, a pressão causada pelo oxigênio é:
a) P = nORT/(2V). b) P
= (nO+nN)RT/(2V). c) P = nORT/V. d) P
= 3nORT/(2V).
P.V =
N.R.T → P = nORT/V.
TERMODINÂMICA
21. (UECE
86.1) Admita uma máquina térmica, funcionando em ciclo de Carnot, sendo de 300
k a temperatura da fonte fria. Se o rendimento dessa máquina é 20%, a
temperatura da fonte quente é:
a)
320 k b) 360 k c) 375 k
d) 395 k
η =
1 – T2/T1 → 0,2 = 1 – 300/T1 → 300/T1
= 0,8 → T1
= 300/0,8 = 375 k.
22. (UECE 91.2) Um gás, encerrado em
uma câmara, sofre uma evolução termodinâmica, percorrendo o ciclo ABCA,
conforme o diagrama abaixo. O trabalho dado pelo gás, ao completar o ciclo, vale,
em Joules:
a) 30 b) 20 c) 10 d) 60
W = b.h/2 = 3.20/2 =
60/2 = 30 J.
23. (UECE
92.2) O tipo de transformação em que é nulo o trabalho efetuado pelo ambiente
sobre o gás é:
a) adiabática b) isobárica c) isotérmica d) isométrica
24. (UECE 2000.1) Através de uma
transformação termodinâmica, uma massa gasosa absorve uma quantidade de calor ∆Q e realiza um trabalho ∆W, sofrendo uma mudança ∆U em sua energia interna. Assinale a alternativa
correta.
a) ∆Q = 0 se a transformação for isotérmica.
b) ∆U = 0 se a transformação for adiabática.
c) ∆U = ∆Q se a
transformação for isovolumétrica.
d) ∆W = 0 se a transformação for isobárica.
25. (UECE
2001.2) Puxa-se lentamente o êmbolo de uma seringa de injeção, que contém ar
aprisionado, da marca 1,0 cm3 até a marca de 1,5 cm3.
Neste processo a pressão variou de 1,0 N/m2 para 0,50 N/m2,
a uma temperatura constante. Sendo de 1,0 cm2 a área da seção
transversal do êmbolo da seringa e supondo que se tenha aplicado uma força
constante de intensidade 3,0 N, a quantidade de calor trocada exclusivamente
neste processo termodinâmico, em joules, é:
a) 1,5x10-2 b) 2,0x10-2 c) 2,5x10-2 d) 3,0x10-2
I. ΔV = A.d → 0,5 = 1.d → d = 0,5 cm = 5.10-3 m.
II. W = F.d = 3.5.10-3
= 1,5x10-2 J.
26. (UECE 2004.2.F2) A
primeira lei da Termodinâmica trata do princípio da conservação de energia em
sistemas termodinâmicos. Ela afirma que uma quantidade de calor ∆Q cedida
a um sistema pode causar uma variação em sua energia interna ∆U ou
realizar um trabalho ∆W sobre ele. Destas três quantidades
expressas na primeira lei:
a) ∆Q independe do processo ocorrido entre o estado inicial e o estado
final.
b) ∆U independe do processo ocorrido entre o
estado inicial e o estado final.
c) ∆W independe do processo ocorrido entre o estado inicial e o estado
final.
d) todas elas dependem do processo ocorrido
entre o estado inicial e o estado final.
27. (UECE 2009.2.F1) Sobre um sistema
que sofre um ciclo termodinâmico completo, conforme ilustrado na figura a
seguir, é correto afirmar que:
a) o trabalho realizado pelo
sistema é nulo.
b) a quantidade de calor trocado
com a vizinhança no ciclo é nula.
c) o trabalho realizado
pelo sistema é igual ao calor trocado no ciclo.
d) o módulo do trabalho realizado
pelo sistema é menor que o calor trocado no ciclo.
É cíclica.(∆U = O e Q = W), como o trabalho
realizado sobre o sistema, então, o gás libera calor para o meio ambiente ( W < 0 e Q < 0). Se o ciclo é anti-horário W < 0.
28. (UECE 2009.2.F2) A figura a
seguir mostra o estado inicial I de um gás ideal e uma isoterma à temperatura T.
Considere que o sistema pode mudar de estado por quatro diferentes processos,
aqui representados por quatro trajetórias, conforme a figura a seguir. O
processo que resulta em aumento da energia interna é:
a) I → 1. b) I → 2. c) I → 3. d) I → 4.
T4 → ∆U = 0
(isotérmico); T2 → ∆U = 0 (isotérmico)
; T1 → ∆U > 0 e T2 < 0.
29. (UECE 2012.1.FASE
2) Um mol de um gás ideal sofre uma expansão isobárica com um correspondente
aumento de temperatura ΔT. Seja
R a constante universal dos
gases. Neste processo, o trabalho por mol realizado pelo gás é
a) (R/ΔT)2. b) RΔT. c) R/ΔT. d) (RΔT)2.
I.
P.V = N.R.ΔT e W = P.V.
II.
W = 1.R.ΔT = R.ΔT.
ÓPTICA
30. (UECE 87.1) Um homem de 2,0 metros de altura coloca-se a
0,5 m de uma câmara escura (de orifício) de comprimento 30 cm. O tamanho da
imagem formada no interior da câmara é:
a) 0,8 m b)
1,0 m c)
1,2 m d) 1,4 m
H/h
= D/d → 2/h = 0,5/0,3 → h = 0,6/0,5 = 1,2 m.
32. (UECE 2004.1.F1) Uma rosa vermelha natural não pode
ser vista por humanos a olho nu num quarto escuro, ao contrário de um filamento
metálico aquecido ao rubro. Isto ocorre porque:
a) a rosa é vermelha e não branca.
b) a luz emitida pelo filamento aquece o olho humano.
c) a rosa não tem luz própria enquanto o
filamento aquecido tem.
d) a rosa vermelha é muito fria comparada com o
filamento aquecido.
Para um objeto ser visto por humanos é
necessário que tal objeto emita luz capaz de sensibilizar os olhos dos humanos.
Esta luz emitida pode ser própria ou através de múltiplas reflexões.
32. (UECE 85.2) Aline completa dez anos de
participação nos vestibulares da UECE. Mira-se diante de um espelho plano e vai
se afastando, perpendicularmente ao espelho, com velocidade uniforme de 10
cm/s. A velocidade com que a imagem se afasta de Aline é:
a) 5 cm/s b) 10 cm/s c) 15 cm/s d) 20 cm/s
Vi = 2.VE
= 2.10 = 20 cm/s.
33. (UECE 90.1) No esquema abaixo, é
mostrado um homem de frente para um espelho plano S, vertical e de costas para
uma árvore P, de altura igual a 4,0 m. Qual deverá ser o comprimento mínimo do
espelho para que o homem possa ver nele a imagem completa da árvore?
a) 0,5 m b) 1,0 m c) 1,5 m d) 2,0 m
x/2 = 4/8 → x = 1 m.
34. (UECE 93.1) A figura ao lado
representa o olho “O” de um observador colocado a uma distância de 2,0 m de um
espelho plano S, e uma lâmpada L colocada à distância de 6,0 m do mesmo
espelho. Um raio luminoso emitido por L reflete-se em S e atinge o olho “O”. A
distância percorrida por esse raio é:
a) 8,0 m b) 10 m c) 12 m d) 14 m
Fazendo as simetrias dos pontos A e B
com o prolongamento dos raios e realizando a reflexão no espelho , teremos dois
triângulos semelhantes ,mas usaremos o teorema de Pitágoras para achar x .
Então x2 = 62 + 82 → x = 10 m.
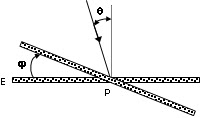
35. (UECE 2000.1) Um raio de luz incide sobre um espelho plano,
representado na figura pela letra E, no ponto P, fazendo um ângulo θ = 10º com a normal. Gira-se o espelho em torno de um
eixo, contido no plano do espelho e que passa por P, de um ângulo de φ = 30º. O raio refletido gira de:
|
q
|
|
j
|
|
E
|
|
P
|
a) 10º b) 20º c) 40º d) 60º
Lembrando que o ângulo de incidência é igual ao
de reflexão e fazendo uma análise geométrica da situação, chega-se a figura
abaixo.
36. (UECE 89.2) Em uma experiência, fez-se
passar um feixe de luz monocromática de ao ar para o benzeno, como é mostrado na
figura ao lado. Através de um disco circular, com o centro na superfície livre
do benzeno, foram medidas as distâncias:
a = 30 cm
b = 20 cm
Conclui-se que o índice de refração do
benzeno, com relação ao ar, é:
a) 1,0 b) 1,5 c) 0,66 d) 2,0
sen i = a/R = 30/R e sen r =
b/R = 20/R, então:
NAR.sen i = NB.sen r → nB,AR = sen i/
sen r = (20/R)/(30/R) = 30/20 = 1,5.
37. (UECE 94.2) A atmosfera terrestre pode
ser considerada, do ponto de vista óptico, como um meio composto por camadas
homogêneas que não refletem, e cujo índice de refração decresce a partir da
superfície. Uma fonte de raio laser emite um raio dirigido para a Lua. A trajetória
que melhor representa esse raio é:
a) I b) II c) III d) IV
Como
o raio vai passando para camadas mais altas, de ar mais rarefeito (menos denso)
e de menor índice de refração, então esse raio deve ir se afastando da normal.
38. (UECE
2002.1) Uma criança faz bolhas de sabão com o auxílio de um canudinho – ou até
mesmo um talo de mamoeiro – soprando água na qual se mistura um pouco de sabão
em pó. Quando a bolha está crescendo, pode-se ver o belo espetáculo da mudança
de cor da película da bolha. Isto ocorre, principalmente, por causa do seguinte
conceito da Óptica.
a) interferência b) polarização c) difração d) absorção
39. (UECE 2008.2.F2) A luz do Sol inclina-se na direção da
superfície da Terra a medida que penetra na atmosfera Como consequência, ainda
podemos ver o Sol, mesmo depois que esse já esta abaixo da linha do horizonte, ao
entardecer. Esse fenômeno dá-se devido a
a) atração da gravidade da terra.
b) variação do índice de refração do ar com a
altitude.
c) dispersão da luz na atmosfera.
d) difração da luz ao penetrar a atmosfera.
O índice de refração da atmosfera muda
continuamente, por isso o raio de luz proveniente do sol curva-se
constantemente e podemos ver o sol mesmo após ele passar pelo horizonte.
40. (UECE 2010.1.F1) Um raio de luz monocromático reduz sua velocidade
em 50 % ao passar do meio I para o meio II. Podemos afirmar que o índice de
refração do meio II é maior que o índice de refração do meio I:
a) 1,3 vezes
b) 1,5 vezes c) 2,0 vezes
d) 2,5 vezes
N2/N1 = V1V2
= V/0,5V = 2 → N2 = 2.N1.
41. (UECE 85.1) Um pequeno objeto
retilíneo é colocado a 10 cm do vértice e perpendicularmente ao eixo principal
de um espelho esférico, côncavo, de pequena abertura e cuja distância focal
mede 20 cm. A imagem formada pelo espelho é:
a) Real, igual e invertida.
b) Real, maior e direita.
c) Virtual, maior e direita.
d) Virtual, menor e invertida.
f = p.p’/(p + p’) → 20 = 10.p’/(10 + p’) → 20 + 2p’ = p’ → p’ = - 20 cm.
42. (UECE 86.1) Uma lente divergente
fornecerá, de um objeto real, uma imagem com as seguintes características:
a) real, invertida e ampliada.
b) real, invertida e diminuída.
c) virtual, direita e ampliada.
d)
virtual, direita e diminuída.
43. (UECE 91.2) Um banco óptico é usado para determinar a
distância focal de uma lente esférica convergente. Na montagem da figura, a
distância do objeto à lente é p = 20 cm e a distância do anteparo à lente é p’
= 80 cm.
Assinale a opção que representa corretamente o valor da
distância focal (f) e o aumento linear obtido.
distância focal (cm)
|
aumento linear
|
|
a)
|
8
|
16
|
b)
|
12
|
4
|
c)
|
16
|
8
|
d)
|
16
|
4
|
f = 20.80/(20 + 80) = 1600/100 = 16 cm.
A = -p’/p = - 80/20 = - 4.
44. (UECE 95.1) No esquema mostrado, a chama de uma vela está
situada no foco F de uma lente convergente L, e E é um espelho plano normal ao
eixo principal da lente. A imagem da chama, conjugada pelo espelho E, funciona
como objeto em relação á lente L. A imagem final, conjugada pela lente, ficará
afastada do centro óptico da lente de:
a) 10 cm b)
15 cm c)
20 cm d) 40 cm
A imagem da vela, que servirá de objeto para a
lente, ficará situada a 5 cm “atrás” do espelho plano, ou seja a 20 cm da
lente; exatamente sobre seu ponto antiprincipal objeto. Sendo assim, a imagem
recairá no ponto antiprincipal imagem, a 20 cm da lente.
45. (UECE
2006.1.F2) A figura ilustra um desenho esquemático de um CD, com uma
ampliação, mostrando parte da trilha em
espiral, cuja largura é menor que 10 microns. O equipamento que faz a leitura
do disco consiste essencialmente de uma fonte de luz e uma lente.
|
lente
|
Como o feixe de luz deve ter seu
diâmetro reduzido à largura de uma trilha no disco, pode-se dizer que a lente
utilizada pode ser do tipo:
a) bicôncava ou biconvexa.
b) plano-côncava.
c) biconvexa.
d) bicôncava.
Essa lente será
de comportamento óptico convergente,
portanto será biconvexa.
46. (UECE 2009.1.F2) Uma estudante constrói uma luneta usando
uma lente convergente de 58,2 cm de distância focal como objetiva e uma lente
convergente com 1,9 cm de distância focal como ocular. Sabendo-se que a
distância entre as lentes ocular e objetiva é de 60 cm, qual é,
aproximadamente, a distância, em centímetros, entre a imagem final de um astro
observado e a ocular?
a) 10,0 b)
30,6 c)
34,2 d) 36,4
I. 1/f1 = 1/p1 + 1/p1’ → 1/58,2 = 1/(infinito) + 1/p1’ → 1/58,2 = 1/p1’ → p1’ = 58,2 cm.
II. p1’ + p2 = 60 → p2 = 1,8 cm.
III. f2 = p2.p2’/(p2
+ p2’) → 1,9 =
1,8.p2’/(1,8 + p2’) → p2’ = - 34,2 cm.
ONDULATÓRIA
47. (UECE 2002.2) Uma rádio FM emite ondas com freqüência de 100 MHz. Se a velocidade de propagação da luz no ar é cerca de 3.108 m/s, o período de oscilação, em s, e o comprimento destas ondas, em m, serão, respectivamente, iguais a:
A) 10-8 e 3
B) 10-8 e 3.10-6
C) 10-2 e 300
D) 10-2 e 3.10-6
V = 3 . 108m/s, f = 100 MHz = 100 . 106Hz
= 108Hz
I. V = λ . f
II. T =
1/f =1/108 = 10-8 s.
48. (UECE 2009.2.F2) A curva que melhor representa a velocidade v(t) contra o
deslocamento x(t) de um oscilador harmônico é
A) uma reta passando pela origem.
B) uma elipse centrada na origem.
C) uma senóide.
D) uma co-senóide.
V(t) = - ω.A.sen(ω.t + φ) e x(t) = A.cos(ω.t + φ),
temos sen(ω.t + φ) = - V/ω.A e cos(ω.t + φ) = x/A. Fazendo sen2(ω.t + φ) + cos2(ω.t
+ φ) = 1, temos V2/(ω.A)2
+ x2/A2 = 1,
lembrando uma elipse cuja equação é dada por x2/a2 + y2/b2 = 1 de
centro (0,0).
49. (UECE 2009.2.F2) Nos itens a seguir, são dadas as equações de quatro ondas
progressivas com x em metros e t em segundos:
I. y(x,t) = sen(2x
– 4t)
II. y(x,t) =
2sen(3x – 3t)
III. y(x,t) =
5sen(2x – 6t)
IV. y(x,t) =
10sen(4x – t)
A onda de maior velocidade de propagação é a do item
A) II. B)
IV. C)
III. D) I.
y =
sen (x/(1/2) – 4.t) → V1
= (1/2).4 = 2 m/s.
y =
sen (x/(1/3) – 3.t) → V2
= (1/3).3 = 1 m/s.
y =
sen (x/(1/2) – 6.t) → V3 = (1/2).6 = 3 m/s.
y =
sen (x/(1/4) – 1.t) → V4
= (1/4).1 = 0,25 m/s.
50. (UECE 92.1) A respeito dos raios
LASER, considere as afirmações:
I. São elétrons ativados.
II. Tem natureza ondulatória.
III. São desviados por campo elétrico.
IV. Sofrem difração.
São corretas:
a) apenas II e III.
b) apenas I e III.
c) apenas I e IV.
d) apenas II e IV.
51. (UECE-98.1) A figura abaixo mostra
duas ondas que se propagam em cordas idênticas (mesma velocidade de
propagação).
É correta a afirmação:
a) frequência em I é menor
que em II e o comprimento de onda em I é maior que em II.
b) a amplitude em ambas é a mesma e a
frequência em I é maior que em II.
c) a frequência e o comprimento de
onda são maiores em I.
d) as freqüências são
iguais e o comprimento de onda é maior em I.
52. (UECE 2004.1.F2) A
figura vista na página seguinte mostra o gráfico de uma onda senoidal
transversal se propagando, com velocidade de 4 m/s, ao longo de uma corda.
Os
valores do comprimento de onda, da amplitude e da freqüência são,
respectivamente:
a) 4 cm, 2 cm, 0,01 Hz.
b) 4 cm, 2 cm, 100 Hz.
c) 4 cm, 2 cm, 10,0 Hz.
d) 2 cm, 4 cm, 100 Hz.
A = 2 cm; λ = 4 cm e v = λ.f
53. (UECE 2009.1.F2) Uma corda de piano de comprimento L, presa
horizontalmente por suas extremidades, está vibrando, verticalmente, com
comprimento de onda igual ao seu comprimento. No instante em que ela se mostra
totalmente na horizontal, a velocidade de cada ponto ao longo da corda é
a) zero em toda extensão da corda.
b) diferente de zero em toda extensão da corda.
c) dependente da posição na corda, sempre na direção
horizontal ou nula.
d) dependente da posição na corda, sempre na
direção vertical ou nula.
A velocidade nos NÓS é nula e nos ventres é
máxima, sendo que muda a cada harmônico, assim dependendo da sua posição na
corda.
54. (UECE 2009.1.F2) Uma onda de luz monocromática se propaga ao longo de um
cano retilíneo com suas extremidades fechadas por espelhos refletores
perfeitos, e em cujo volume interno existe vácuo. Uma onda estacionária de
freqüência f e comprimento de onda λ é formada. Se um gás de índice de
refração n for introduzido no cano,
qual entre as seguintes mudanças ocorre?
A) λ aumenta.
B) λ diminui.
C) f aumenta.
D) f diminui.
Ao ser introduzido um gás no cano, o que mudará
na onda é o comprimento de onda (λ) e sua velocidade (V), mantendo-se a
frequência constante, como no vácuo temos a maior velocidade para essa onda luminosa e V = λ.f, logo no gás a velocidade
diminui assim como o seu comprimento de onda.
55. (UECE 2000.2) Considere o observador (O) e a
sirene (S) que emite som de frequência 600 Hz, vistos na figura.
O ouvido de (O) se encontra no
mesmo plano do momento circular e uniforme descrito por (S). A máxima variação
da frequência do som, em Hz, ouvido por (O), suposto em repouso em relação ao
eixo do movimiento circular de (S). é:
a) 44 b) 42 c) 40 d) 38
I. VF = ω.R
= 50.0,2 = 10 m/s.
II. Usando a fórmula
do efeito doppler : fMÁX = f.V/(V – VF) = 600.330/(330 –
10) = 618,75 Hz.
56. (UECE 85.1) Dentre as seguintes ondas
eletromagnéticas, as que apresentam maior comprimento de onda são:
a) Raios gama b) Raios X c) Raios infravermelhos d) Microondas
57. (UECE 98.2) O nível de
intensidade sonora é definida por β = 10 log I/I0
(decibel) em que I é a intensidade sonora da onda e I0 é a
intensidade do mais fraco som audível. Numa festa,todos os presentes falam com
a mesma intensidade I.Se apenas uma pessoa estivesse falando,o nível de
intensidade sonora do ruído seria de 60 dB.Se as 100 pessoas presentes falarem
ao mesmo tempo,o nível de intensidade sonora do ruído será:
a) 60 dB b) 80 dB c) 100 dB d) 600 dB
I. N =10.Log(I/I0) = 60 dB.
II.
N’ = 10.Log(100.I/I0) = 10.Log100 + 10.Log(I/I0) = 20 +
60 = 80 dB.
58. (UECE 2009.1.F1) Para uma corda de piano de
comprimento L, as possíveis ondas estacionárias de menor freqüência têm
comprimentos de onda iguais a:
a) 2L, L e 1/2 L.
b) 3L, 2L e L.
c) 2L, L e 2/3 L.
d) L, 3/2 L e 1/3 L.
λ1 = 2L/N = 2L/1 = 2L; λ2 = 2L/N
= 2L/2 = L e λ3 = 2L/N = 2L/3.
59. (UECE 99.2) O efeito Doppler pode
ser usado para medir a:
a) distância de uma estrela à Terra.
b) velocidade radial de uma
estrela, em relação à Terra.
c) massa de uma estrela.
d) temperatura de uma estrela.
60. (UECE 94.2) Toca-se sucessivamente em
duas teclas de um piano, a primeira corresponde a nota mi, e a segunda a nota
sol. Ouve-se assim dois sons diferentes, porque as ondas sonoras que
correspondem a estas notas têm:
a) amplitudes diferentes.
b) freqüências diferentes.
c) intensidades diferentes.
d) timbres diferentes.


























Professor, quais assuntos caem com frequência na UECE??
ResponderExcluirO material ta muito show.
ResponderExcluirParabéns pelo trabalho
Excluirna questão 13
ResponderExcluira unidade de temperatura do calor específico está em kelvin
não teríamos que transformar o 0,72 em °C ?